Investment Irreversibility

Overview

Investment irreversibility is a prominent theme in theories of investment. When asset specificity is higher, disinvestment is more costly and irreversibility is stronger. We document that disinvestment is indeed less common in such cases, which verifies that disinvestment frictions are more severe. We then show how asset specificity shapes the impact of uncertainty on investment activities.

Prevalence of Disinvestment

When assets have high specificity and low liquidation values, firms lose more from directly selling these assets. Accordingly, we should expect a lower prevalence of asset sales on a standalone basis. The figure shows that the average frequency of PPE sales per year (y-axis) is lower for industries with lower PPE liquidation recovery rate (the x-axis). Similar result holds if we use PPE liquidation recovery rate predicted by physical attributes.

Investment Response to Uncertainty

A further implication of investment irreversibility is that uncertainty negatively affects investment activities (see Bloom (2014) for a summary). We use the following firm-level annual regression to study how the investment response to uncertainty varies with the degree of asset specificity:

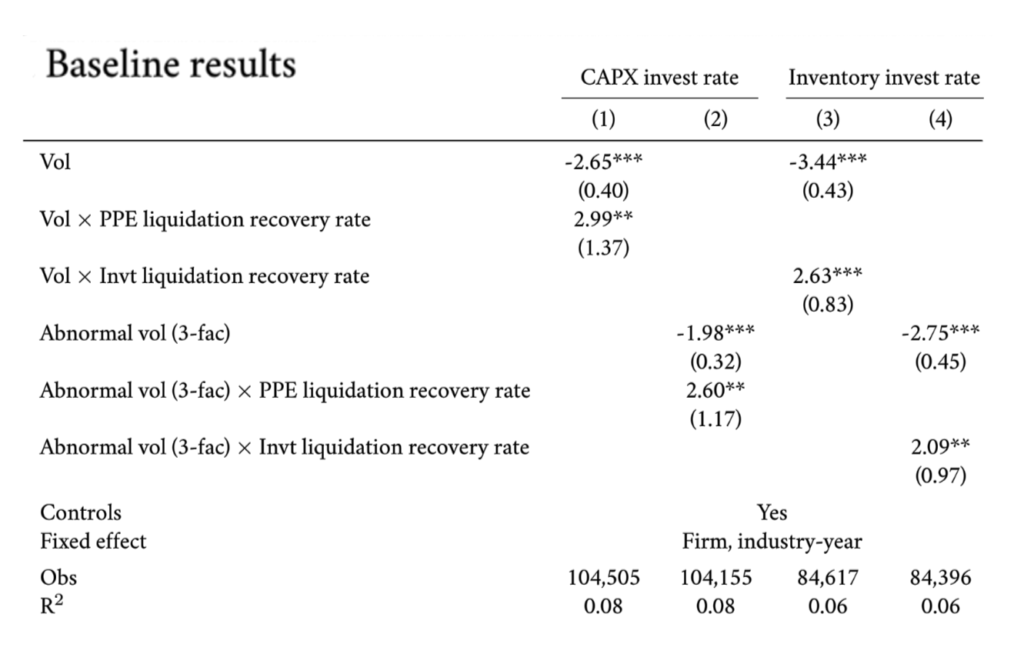
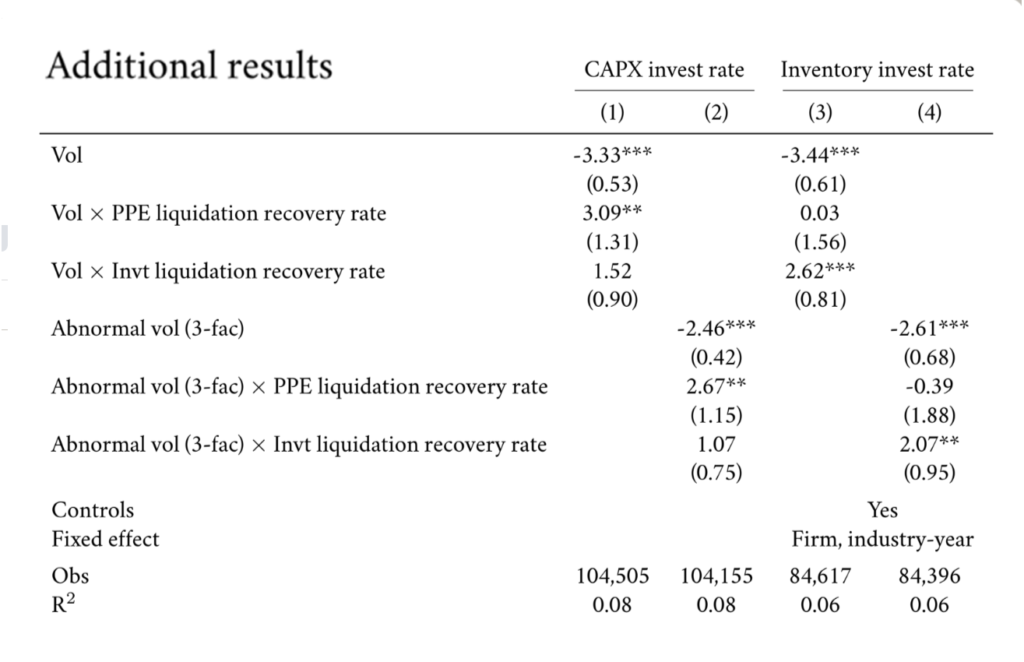
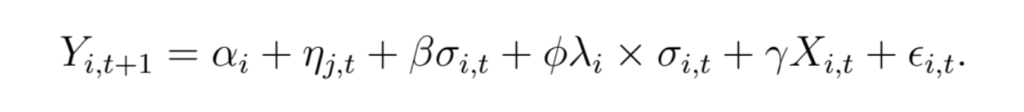For the uncertainty measure σi,t, we use both the daily volatility of a firm’s stock returns over the previous year and the volatility of abnormal returns (based on the Fama-French three factor model) a la Gilchrist, Sim, and Zakrajšek (2014). The liquidation recovery rate is denoted by λi, which is matched to Compustat firms based on their industries. The outcome Yi,t+1 is the investment rate in year t+1 to allow for lags in investment implementation (Lamont, 2000). This specification also alleviates concerns about a reverse impact of investment behavior on stock return volatility. The control variables X include Q, book leverage, cash holdings, EBITDA, size (log book assets), and ratings at the end of year t, as well as the level of stock returns in year t and its interaction with λ. We include firm fixed effects (αi) and industry-year fixed effects (ɳ j,t), and double-cluster standard errors by firm and time. We use a longer sample of 1980 to 2016 to allow for more variation in uncertainty over time.

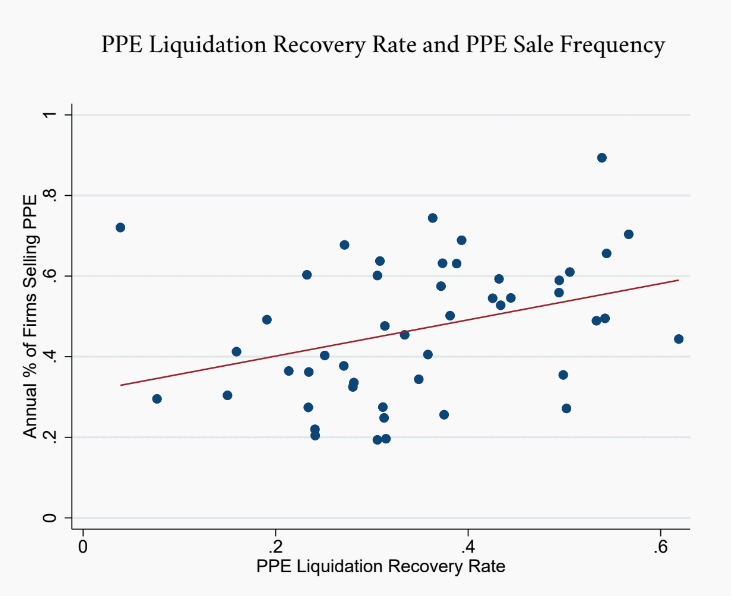
We start with capital expenditures (i.e., investment in PPE) as the outcome variable, normalized by lagged net PPE. In this case, we use the PPE liquidation recovery rate for λ. We find that higher uncertainty is associated with significant decreases in capital expenditures when the PPE liquidation recovery rate is low, but not when the PPE liquidation recovery rate is high. Indeed, when the PPE liquidation recovery rate is zero, the coefficient on volatility (β) is significantly negative; when the PPE liquidation recovery rate is one, the coefficient on volatility (β+Φ) becomes roughly zero. This result matches closely with theoretical predictions and indicates that asset specificity is key to the negative impact of uncertainty on firm investment.

We also study inventory investment, which can also play an important role for economic fluctuations (see Ramey and West (1999) for a summary). We use inventory the liquidation recovery rate for λ and interact it with the uncertainty measure σ. We find that higher uncertainty is also associated with significant decreases in inventory investment when the inventory liquidation recovery rate is low, but not when the inventory recovery rate is high. Again, the response to uncertainty is roughly zero if inventory is fully generic (i.e., when the inventory liquidation recovery rate is one).

Furthermore, we find that the impact of uncertainty on fixed asset investment is mainly affected by PPE liquidation recovery rates, while inventory liquidation recovery rates have a weaker impact. Conversely, the impact of uncertainty on inventory investment is affected by inventory liquidation recovery rates, but not by PPE liquidation recovery rates. In other words, there is a precise mapping between the specificity of one type of assets and its investment sensitivity to uncertainty.